BAB 3
UKURAN PEMUSATAN
Ukuran pemusatan memberikan gambaran pemusatan pada data.
1.Rataan (Mean)
Adalah jumlah semua nilai pengamatan
dibandingkan dengan banyaknya pengamatan.
2.Nilai Tengah (Median)
Adalah sebuah nilai pengamatan yang berada
di tengah-tengah nilai pengamatan keseluruhan yang telah diurutkan.
Untuk data dengan n ganjil maka median adalah
Untuk data dengan n genap maka median
adalah
3.Modus
Adalah data pengamatan yang paling sering
muncul di keseluruhan data pengataman. Suatu data pengamatan mungkin memiliki
modus atau tidak. Dan mungkin memiliki modus lebih dari satu.
4.Quartil
Adalah pembagian data menjadi empat bagian
yang sama besar banyak datanya.
Terdiri dari kuartil bawah, tengah dan
atas. (Jumlah data > 4).
5.Desil
Adalah pembagian data menjadi sepuluh bagian
yang sama besar banyak datanya. (Jumlah data > 10).Dalam distribusi normal, kedua ukuran ini sangat dibutuhkan. Nilai rata-rata (mean) untuk ukuran pemusatan, hal ini berguna untuk mengetahui nilai tengah dari kurva normal dan nilai simpangan baku untuk ukuran penyebaran, hal ini berguna untuk mengetahui lebar dari kurva normal tersebut.
Ada namanya Statistik Lima Serangkai , yaitu
Perlakuan pada ukuran pemusatan dapat mengakibatkan, sebagai berikut :
- Setiap perlakuan data awal : (+) ; (-) ; (x) ; (:) dengan suatu bilangan k maka akan mengubah ukuran pemusatan awal dengan memberikan perlakuan : (+) ; (-) ; (x) ; (:) sebesar bilangan k tersebut kepada ukuran pemusatan awal.
- Setiap perlakuan data awal : (+) atau (-) dengan suatu bilangan k maka ukuran penyebaran data awal tidak akan berubah.
- Setiap perlakuan data awal : (x) atau (:) dengan suatu bilangan k maka akan mengubah ukuran penyebaran data awal dengan memberikan perlakuan : (x) atau (:) sebesar bilangan k tersebut kepada ukuran penyebaran awal.
Contoh :
Suatu sekolah memiliki nilai hasil UN dengan rata-rata 40, median 45 dan simpangan kuartil 10.
Karena rata-rata terlalu rendah maka semua nilai dikalikan dengan 2 kemudian dikurangi 15. Akibatnya adalah :
Ukuran pemusatan dalam kasus ini adalah rata-rata dan median.
Semua perlakuan tidak akan mengubah ukuran pemusatannya. Sehingga nilai rata-rata tetap 40 dan nilai median tetap 45.Ukuran penyebaran dalam kasus di atas adalah simpangan baku.
Jika simpangan baku dikalikan dengan dua, maka ukuran penyebaran yang baru akan dikalikan dua jadi simpangan bakunya adalah 20, dan selanjutnya dikurangi 15, hal ini tidak akan berpengaruh. Sehingga nilai simpangan baku adalah 20.
BAB 4
UKURAN PENYIMPANGAN
PENGUKURAN PENYIMPANGAN
Pengukuran penyimpangan adalah suatu
ukuran yang menunjukkan tinggi rendahnya perbedaan data yang diperoleh
dari rata-ratanya. Ukuran penyimpangan digunakan untuk mengetahui luas
penyimpangan data atau homogenitas data. Dua variabel data yang memiliki
mean sama belum tentu memiliki kualitas yang sama, tergantung dari
besar atau kecil ukuran penyebaran datanya. Ada bebarapa macam ukuran
penyebaran data, namun yang umum digunakan adalah standar deviasi.
Macam-macam ukuran penyimpangan data adalah :
- Jangkauan (range)
- Simpangan rata-rata (mean deviation)
- Simpangan baku (standard deviation)
- Varians (variance)
- Koefisien variasi (Coefficient of variation)
1. Jangkauan (range)
Range adalah salah satu ukuran statistik
yang menunjukan jarak penyebaran data antara nilai terendah (Xmin)
dengan nilai tertinggi (Xmax). Ukuran ini sudah digunakan pada
pembahasan daftar distribusi frekuensi. Adapun rumusnya adalah
Contoh : Berikut ini nilai ujian semester dari 3 mahasiswa
A = 60 55 70 65 50 80 40
B = 50 55 60 65 70 65 55
C = 60 60 60 60 60 60 60
Dari data diatas dapat diketahui bahwa
A = memiliki Xmax=80, Xmin= 40 , R = 40 , meanya 60
B = memiliki Xmax=70, Xmin= 50 , R = 20 , meanya 60
C = memiliki Xmax=60, Xmin= 60 , R = 0 , meanya 60
Dari contoh di atas dapat disimpulkan bahwa :
a. Semakin kecil rangenya maka semakin homogen distribusinya
b. Semakin besar rangenya maka semakin heterogen distribusinya
c. Semakin kecil rangenya, maka meannya merupakan wakil yang representatif
d. Semakin besar rangenya maka meannya semakin kurang representatif
2. Simpangan Rata-rata (mean deviation)
Simpangan rata-rata merupakan
penyimpangan nilai-nilai individu dari nilai rata-ratanya. Rata-rata
bisa berupa mean atau median. Untuk data mentah simpangan rata-rata dari
median cukup kecil sehingga simpangan ini dianggap paling sesuai untuk
data mentah. Namun pada umumnya, simpangan rata-rata yang dihitung dari
mean yang sering digunakan untuk nilai simpangan rata-rata.
- Data tunggal dengan seluruh skornya berfrekuensi satu
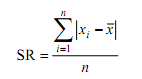
dimana xi merupakan nilai data
- Data tunggal sebagian atau seluluh skornya berfrekuensi lebih dari satu
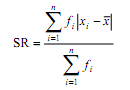
dimana xi merupakan nilai data
- Data kelompok ( dalam distribusi frekuensi)
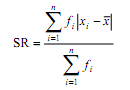
dimana xi merupakan tanda kelas dari interval ke-i dan fi merupakan frekuensi interval ke-i
Contoh :Dari tabel diperoleh
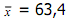
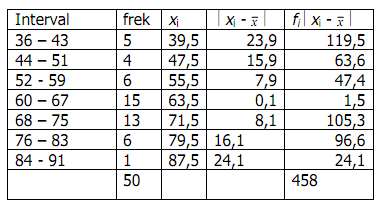
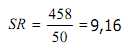
Standar deviasi merupakan ukuran
penyebaran yang paling banyak digunakan. Semua gugus data
dipertimbangkan sehingga lebih stabil dibandingkan dengan ukuran
lainnya. Namun, apabila dalam gugus data tersebut terdapat nilai
ekstrem, standar deviasi menjadi tidak sensitif lagi, sama halnya
seperti mean.
Standar Deviasi memiliki beberapa
karakteristik khusus lainnya. SD tidak berubah apabila setiap unsur pada
gugus datanya di tambahkan atau dikurangkan dengan nilai konstan
tertentu. SD berubah apabila setiap unsur pada gugus datanya
dikali/dibagi dengan nilai konstan tertentu. Bila dikalikan dengan nilai
konstan, standar deviasi yang dihasilkan akan setara dengan hasilkali
dari nilai standar deviasi aktual dengan konstan.
Rumus Simpangan Baku untuk Data Tunggal
- untuk data sample menggunakan rumus
- untuk data populasi menggunkan rumus
Contoh :
Selama 10 kali ulangan semester ini sobat mendapat nilai 91, 79, 86, 80, 75, 100, 87, 93, 90,dan 88. Berapa simpangan baku dari nilai ulangan sobat?
JawabSelama 10 kali ulangan semester ini sobat mendapat nilai 91, 79, 86, 80, 75, 100, 87, 93, 90,dan 88. Berapa simpangan baku dari nilai ulangan sobat?
Soal di atas menanyakan simpangan baku dari data populasi jadi menggunakan rumus simpangan baku untuk populasi.
Kita cari dulu rata-ratanya
rata-rata = (91+79+86+80+75+100+87+93+90+88)/10 = 869/10 = 85,9
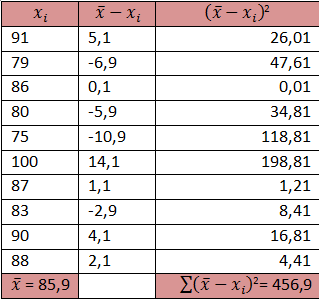
Kita masukkan ke rumus
Rumus Simpangan Baku Untuk Data Kelompok
- untuk sample menggunakan rumus
- untuk populasi menggunakan rumus
Contoh :
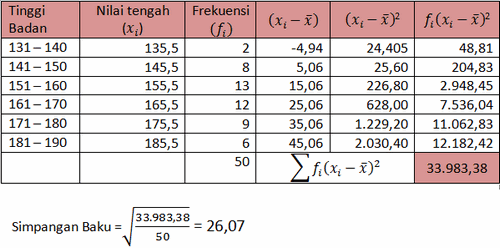
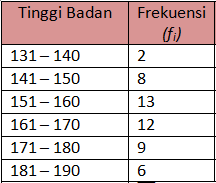
Diketahui data tinggi badan 50 siswa samapta kelas c adalah sebagai berikut
hitunglah berapa simpangan bakunyaDiketahui data tinggi badan 50 siswa samapta kelas c adalah sebagai berikut
1. Kita cari dulu rata-rata data kelompok tersebut
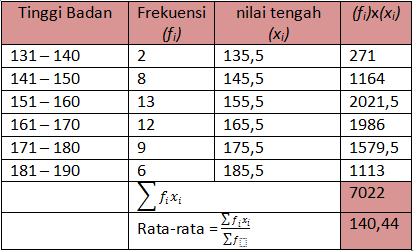
2. Setelah ketemu rata-rata dari data kelompok tersebut kita bikin tabel untuk memasukkannya ke rumus simpangan baku
4. Varians (variance)
Varians adalah salah satu
ukuran dispersi atau ukuran variasi. Varians dapat menggambarkan
bagaimana berpencarnya suatu data kuantitatif. Varians diberi simbol σ2 (baca: sigma kuadrat) untuk populasi dan untuk s2 sampel.
Selanjutnya kita akan menggunakan simbol s2 untuk varians karena umumnya kita hampir selalu berkutat dengan sampel dan jarang sekali berkecimpung dengan populasi.
Rumus varian atau ragam data tunggal untuk populasi
Rumus varian atau ragam data tunggal untuk sampel
Rumus varian atau ragam data kelompok untuk populasi
Rumus varian atau ragam data kelompok untuk sampel
Keterangan:
σ2 = varians atau ragam untuk populasi
S2 = varians atau ragam untuk sampel
fi = Frekuensi
xi = Titik tengah
x¯ = Rata-rata (mean) sampel dan μ = rata-rata populasi
n = Jumlah data
σ2 = varians atau ragam untuk populasi
S2 = varians atau ragam untuk sampel
fi = Frekuensi
xi = Titik tengah
x¯ = Rata-rata (mean) sampel dan μ = rata-rata populasi
n = Jumlah data
5. Koefisien variasi (Coefficient of variation)
Koefisien variasi merupakan suatu ukuran
variansi yang dapat digunakan untuk membandingkan suatu distribusi data
yang mempunyai satuan yang berbeda. Kalau kita membandingkan berbagai
variansi atau dua variabel yang mempunyai satuan yang berbeda maka tidak
dapat dilakukan dengan menghitung ukuran penyebaran yang sifatnya
absolut.
Koefisien variasi adalah suatu perbandingan antara simpangan baku dengan nilai rata-rata dan dinyatakan dengan persentase.


Besarnya koefisien variasi akan
berpengaruh terhadap kualitas sebaran data. Jadi jika koefisien variasi
semakin kecil maka datanya semakin homogen dan jika koefisien korelasi
semakin besar maka datanya semakin heterogen.
Daftas Pustaka :
Suharyadi, & Purwanto. (2009). In Statistika untuk Ekonomi dan Keuangan Modern. Jakarta: Salemba Empat.
BAB 5
MOMEN KEMIRINGAN DAN KURTOSIS
Ukuran Kemiringan (skewness)
Merupakan derajat atau ukuran dari ketidaksimetrisan (Asimetri) suatu distribusi data. Kemiringan distribusi data terdapat 3 jenis, yaitu :
Simetris : menunjukkan letak nilai rata-rata hitung,
median, dan modus berhimpit (berkisar disatu
titik)
Miring ke kanan : mempunyai nilai modus paling
kecil dan rata-rata hitung
paling besar
Miring ke kiri : mempunyai nilai modus paling
besar dan rata-rata hitung paling kecil
Untuk mengukur derajat kecondongan suatu distribusi dinyatakan dengan koefisien kecondongan (koefisien skewness).Ada tiga metode yang bisa digunakan untuk menghitung koefisien skewness yaitu :
Rumus pearson
= 1/S (X ̅ - Mod) Atau = 3/S (X ̅ – Med)
Rumus Momen
Data tidak berkelompok
3 = 1/〖nS〗^2 ∑ ( X1 X ̅ )3
Data Berkelompok
3 = 1/〖nS〗^3 ∑f i( mi - X ̅ )3
Keterangan
3 = derajat kemiringan
x1 = nilai data ke – i
X ̅ = nilai rata-rata hitung
Fi = frrekuensi nilai ke i
M1 = nilai titik tengah kelas ke-i
S = Simpangan Baku
N = Banyaknya data
Jika 3 = 0 distribusi data simetris
3 < 0 distribusi data miring ke kiri
3 > 0 distribusi data miring ke kanan
Rumus bowley
Rumus ini menggunakan nilai kuartil :
3 = (Q_3+ Q_1- 2Q_2)/(Q_3- Q_1 )
Keterangan :
Q1 = kuartil pertama
Q2 = Kuartil Kedua
Q3 = Kuaril Ketiga
Cara menentukan kemiringannya :
Jika Q3 – Q2 = Q2 – Q1 sehingga Q3 + Q1 -2Q2 = 0 yang mengakiibatkan 3 = 0, sebaliknya jika distribusi miring maka ada dua kemungkinan yaitu Q1 = Q2 atau Q2 = Q3, dalam hal Q1 = Q2 maka 3 = 1 , dan untuk Q2 = Q3 maka 3 = -1
Ukuran kemiringan data merupakan ukuran yang menunjukan apakah penyebaran data terhadap nilai rata-ratanya bersifat simetris atau tidak. Ukuran kemiringan pada dasarnya merupakan ukuran yang menjelaskan besarnya penyimpangan data dari bentuk simetris. Suat distribusi frekuensi yang miring (tidak simetris) akan memiliki nilai mean, median dan modus yang tidak sama besar (X ̅ ≠ Md ≠ Mo) sehinggan distribusi akan memusat pada salah satu sisi yaitu sisi kanan atau sisi kiri. Hal ini yang menyebabkan bentuk kurva akan miring ke kanan atau ke kiri. Jika kurva miring ke arah kanan (ekornya memanjang ke arah kiri) disebut kemiringan positif, dan jika kurva miring ke arah kiri (ekornya memnjang ke arah kanan) disebut kemiringan negatif.
Analisis kasus :
Tabel 2.1
Cara perhitungan koefisien kecondongan dengan metode
Pearson dari data penghasilan keluarga
penghasila keluarga X f U fU Fu2
10-22 16 5 -3 -15 225
23-35 29 6 -2 -12 144
36-48 42 13 -1 -13 169
49-61 55 19 0 0 0
62-74 68 11 1 11 121
75-87 81 11 2 22 484
88-100 94 5 3 15 225
Jumlah 70 ∑ fU = 8 ∑ fU2 = 1368
Sebelum menggunakan rumus terlebih dahulu dicari nilai , mean, median, dan standar deviasinya berikut ini:
Mean :
X ̅ = A + ((∑▒〖f.U〗)/n) . i
X ̅ = 55 + (8/70) . 3
X ̅ = 56,485
Median :
Med = Tkbmd + ((1/2 n-fkb)/fmd) . i
Med = 48.5 + ((35-24)/19) . 13
Med = 48.5 + 7,526
Med = 56,026
Standar Deviasi :
S = i √((n∑f.U^2-(∑f.U^2))/(n(n-1)))
S = 13 √(((70)-(1368)-(〖8)〗^2)/(70(70-1)))
S = 13 √19,81
S = 57,86
Setelah kita dapatkan nilai-nilai diatas, kemudian dimasukan ke dalam rumus koefisein skewness :
α = 3/S (X ̅ - Med)
α = 3/57,86 ( 56,485 – 56,026)
α = 0,0238
dari hasil perhitungan menunjukan bahwa koefisien skewness menghasilkan nilai positif, itu berarti distribusi frekuensi mempunyai bentuk kemiringan yang positif yaitu miring ke arah kanan.
Merupakan derajat atau ukuran dari ketidaksimetrisan (Asimetri) suatu distribusi data. Kemiringan distribusi data terdapat 3 jenis, yaitu :
Simetris : menunjukkan letak nilai rata-rata hitung,
median, dan modus berhimpit (berkisar disatu
titik)
Miring ke kanan : mempunyai nilai modus paling
kecil dan rata-rata hitung
paling besar
Miring ke kiri : mempunyai nilai modus paling
besar dan rata-rata hitung paling kecil
Kemiringan simetri (normal) kemiringan Negatif positif
Untuk mengukur derajat kecondongan suatu distribusi dinyatakan dengan koefisien kecondongan (koefisien skewness).Ada tiga metode yang bisa digunakan untuk menghitung koefisien skewness yaitu :
Rumus pearson
= 1/S (X ̅ - Mod) Atau = 3/S (X ̅ – Med)
Rumus Momen
Data tidak berkelompok
3 = 1/〖nS〗^2 ∑ ( X1 X ̅ )3
Data Berkelompok
3 = 1/〖nS〗^3 ∑f i( mi - X ̅ )3
Keterangan
3 = derajat kemiringan
x1 = nilai data ke – i
X ̅ = nilai rata-rata hitung
Fi = frrekuensi nilai ke i
M1 = nilai titik tengah kelas ke-i
S = Simpangan Baku
N = Banyaknya data
Jika 3 = 0 distribusi data simetris
3 < 0 distribusi data miring ke kiri
3 > 0 distribusi data miring ke kanan
Rumus bowley
Rumus ini menggunakan nilai kuartil :
3 = (Q_3+ Q_1- 2Q_2)/(Q_3- Q_1 )
Keterangan :
Q1 = kuartil pertama
Q2 = Kuartil Kedua
Q3 = Kuaril Ketiga
Cara menentukan kemiringannya :
Jika Q3 – Q2 = Q2 – Q1 sehingga Q3 + Q1 -2Q2 = 0 yang mengakiibatkan 3 = 0, sebaliknya jika distribusi miring maka ada dua kemungkinan yaitu Q1 = Q2 atau Q2 = Q3, dalam hal Q1 = Q2 maka 3 = 1 , dan untuk Q2 = Q3 maka 3 = -1
Ukuran kemiringan data merupakan ukuran yang menunjukan apakah penyebaran data terhadap nilai rata-ratanya bersifat simetris atau tidak. Ukuran kemiringan pada dasarnya merupakan ukuran yang menjelaskan besarnya penyimpangan data dari bentuk simetris. Suat distribusi frekuensi yang miring (tidak simetris) akan memiliki nilai mean, median dan modus yang tidak sama besar (X ̅ ≠ Md ≠ Mo) sehinggan distribusi akan memusat pada salah satu sisi yaitu sisi kanan atau sisi kiri. Hal ini yang menyebabkan bentuk kurva akan miring ke kanan atau ke kiri. Jika kurva miring ke arah kanan (ekornya memanjang ke arah kiri) disebut kemiringan positif, dan jika kurva miring ke arah kiri (ekornya memnjang ke arah kanan) disebut kemiringan negatif.
Analisis kasus :
Tabel 2.1
Cara perhitungan koefisien kecondongan dengan metode
Pearson dari data penghasilan keluarga
penghasila keluarga X f U fU Fu2
10-22 16 5 -3 -15 225
23-35 29 6 -2 -12 144
36-48 42 13 -1 -13 169
49-61 55 19 0 0 0
62-74 68 11 1 11 121
75-87 81 11 2 22 484
88-100 94 5 3 15 225
Jumlah 70 ∑ fU = 8 ∑ fU2 = 1368
Sebelum menggunakan rumus terlebih dahulu dicari nilai , mean, median, dan standar deviasinya berikut ini:
Mean :
X ̅ = A + ((∑▒〖f.U〗)/n) . i
X ̅ = 55 + (8/70) . 3
X ̅ = 56,485
Median :
Med = Tkbmd + ((1/2 n-fkb)/fmd) . i
Med = 48.5 + ((35-24)/19) . 13
Med = 48.5 + 7,526
Med = 56,026
Standar Deviasi :
S = i √((n∑f.U^2-(∑f.U^2))/(n(n-1)))
S = 13 √(((70)-(1368)-(〖8)〗^2)/(70(70-1)))
S = 13 √19,81
S = 57,86
Setelah kita dapatkan nilai-nilai diatas, kemudian dimasukan ke dalam rumus koefisein skewness :
α = 3/S (X ̅ - Med)
α = 3/57,86 ( 56,485 – 56,026)
α = 0,0238
dari hasil perhitungan menunjukan bahwa koefisien skewness menghasilkan nilai positif, itu berarti distribusi frekuensi mempunyai bentuk kemiringan yang positif yaitu miring ke arah kanan.
Ukuran Keruncingan (kurtosis)
Merupakan derajat atau ukuran tinggi rendahnya puncak suatu distribusi data terhadap distribusi normalnya data. Jika bentuk kurva runcingberarti nilai data terkonsentrasi terhadap nilai rata-tata atau nilai penyebarannya kecil, sebaliknya jika bentuk kurva nya tumpul berarti nilai data tersebar terhadap nilai rata-rata atau nilai penyebaran besar. Keruncingan distribusi data ini disebut juga kurtosis.
Derajat keruncingan suatu distribusi frekuensi dapat dibedakan menjadi tiga, yaitu:
Leptokurtis
Distribusi data yang puncaknya relatif tinggi atau bentuk distribusi yang ujungnya sangat runcing
Mesokurtis
Distribusi data yang puncaknya tidak terlalu runcing atau tidak terlalu tumpul
Platikurtis
Distribusi data yang puncaknya terlalu rendah atau terlalu mendatar
Mesokurtis leptokurtis platikurtis
Derajat keruncingan distribusi data α4 dapat dihitung berdasarkan rumus berikut
Data tidak berkelompok
α4 = 1/(nS^4 ) ∑ ( Xi - X ̅)4
Data berkelompok
α4 = 1/(nS^4 ) ∑ fi ( mi - X ̅ )4
Keterangan :
α4 = Derajat keruncingan
Xi = nilai data ke – i
= nilai rata-rata hitung
fi = frekuensi kelas ke – i
mi = nilai titik tengah ke –i
S = simpangan baku
n = banyaknya data
dari penggunaan rumus diatas akan menghasilkan kemungkinan tiga nilai yaitu :
α4 = 3 distribusi keruncingan data disebut mesokurtis
α4 > 3 distribusi keruncingan data disebut leptokurtis
α4 < 3 distribusi keruncingan data disebut platikurtis
Analisis kasus :
Tabel 2.2
Cara perhitungan koofisien keruncingan
Dari data penghasilan keluarga
Penghasilan keluarga Frekuensi U f.U f.U2 f.U3 f.U4
10-22 5 -3 -15 45 -135 405
23-35 6 -2 -12 24 -48 96
36-48 13 -1 -13 13 -13 13
49-61 19 0 0 0 0 0
62-74 11 1 11 11 11 11
75-87 11 2 22 44 88 176
88-100 5 3 15 45 135 405
jumlah 70 8 182 38 1106
s = i √((n∑fU^2-(∑f.〖U)〗^2)/(n(n-1)))
s = 13 √(((70)(1368)-(〖8)〗^2)/(70(70-1)))
s = 13 √19,81
s = 57,86
Setelah kita dapatkan nilai diatas, kemudian dimasukan ke dalam rumus koefisein kurtosis :
α4 = [(∑f.U^4)/n-4{(∑f.U^3)/n}{(∑f.U^ )/n}+6{(∑f〖.U〗^2)/n} {(∑f.U)/n}^2-3{(∑f.U)/n}^4 ] i^4/s^4
α4 = [1106/70-4{38/70}{8/70}+6{182/70} {8/70}^2-3{8/70}^4 ] 〖13〗^4/〖57.86〗^4
α4 = (15.7557) (0,00255)
α4 = 0.040
BAB 6
DISTRIBUSI NORMAL, DISTRIBUSI F DAN DISTRIBUSI T
Distribusi normal merupakan salah satu distribusi probabilitas yang penting dalam analisis statistika. Distribusi ini memiliki parameter berupa mean dan simpangan baku. Distribusi normal dengan mean = 0 dan simpangan baku = 1 disebut dengan distribusi normal standar. Apabila digambarkan dalam grafik, kurva distribusi normal berbentuk seperti genta (bell-shaped) yang simetris. Perhatikan kurva distribusi normal normal standar berikut:
Secara matematis, probabilitas distribusi normal standar kumulatif dapat dihitung dengan menggunakan rumus:
Akan tetapi, kita lebih mudah dengan bantuan tabel distribusi normal. Berikut adalah tabel distribusi normal standar, untuk P (X < x), atau dapat diilustrasikan dengan luas kurva normal standar dari X = minus takhingga sampai dengan X = x.
Sumbu X (horizontal) memiliki range (rentang) dari minus takhingga (‒∞) hingga positif takhingga (+∞).
Kurva normal memiliki puncak pada X = 0. Perlu diketahui bahwa luas
kurva normal adalah satu (sebagaimana konsep probabilitas). Dengan
demikian, luas kurva normal pada sisi kiri = 0,5; demikian pula luas
kurva normal pada sisi kanan = 0,5.
Dalam analisis statistika, seringkali kita menentukan probabilitas kumulatif yang dilambangkan dengan notasi P (X<x). Sebagai contoh, P (X<1), apabila diilustrasikan dengan grafik adalah luas kurva normal dari minus takhingga hingga X = 1.
Secara matematis, probabilitas distribusi normal standar kumulatif dapat dihitung dengan menggunakan rumus:
Akan tetapi, kita lebih mudah dengan bantuan tabel distribusi normal. Berikut adalah tabel distribusi normal standar, untuk P (X < x), atau dapat diilustrasikan dengan luas kurva normal standar dari X = minus takhingga sampai dengan X = x.
Distribusi F,
Jika uji t digunakan untuk pengujian dua sampel, uji F atau Anova digunakan untuk pengujian lebih dari dua sampel.
Distribusi F digunakan untuk menguji hipotesis, apakah variansi dari sebuah populasi normal sama dengan variansi dari populasi normal lainnya. Satu variansi sampel yang lebih besar ditempatkan pada pembilang, sehingga rasio minimalnya adalah 1,00. Distribusi F juga digunakan untuk menguji asumsi-asumsi bagi beberapa statistik uji.
Berdasarkan pendapat Douglas A. Lind (2005, p387-388), Distribusi F memiliki ciri-ciri sebagai berikut:
- Terdapat suatu keluarga distribusi F.
Suatu anggota keluarga distribusi F di tentukan berdasarkan dua parameter : derajat kebebasan pada pembilang dan derajat kebebasan pada penyebut.
- Distribusi F bersifat kontinu.
- Distribusi F tidak dapat bernilai negatif.
- Bentuknya tidak simetris.
- Bersifat Asimtotik (Asymptotic).
Distribusi F memberikan sebuah perangkat untuk menjalankan suatu uji variansi dari dua populasi normal. Menentukan validasi sebuah asumsi untuk suatu statistik uji, mula-mula kita tetap harus menentukan hipotesis nolnya. Hipotesis nolnya adalah bahwa variansi dari suatu populasi (σ1²), sama dengan variansi dari populasi normal lainnya (σ2²). Hipotesis alternatifnya dapat berupa perbedaan variansi tersebut.
Distribusi T
Distribusi t merupakan salah satu pengembangan dari Distribusi z. Secara prinsip penggunaan Distribusi t digunakan untuk membandingkan rata-rata dari dua sampel. Rata-rata dua sampel tersebut dibandingkan untuk mengetahui apakah dua data tersebut mempunyai beda. Distribusi biasanya digunakan untuk data yang banyak sampelnya kurang dari sama dengan 30.




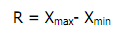
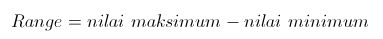
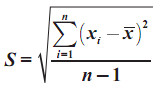
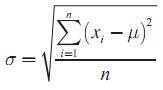
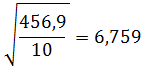
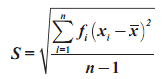
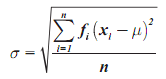
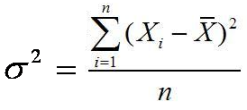
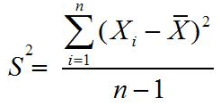
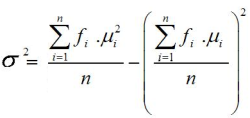
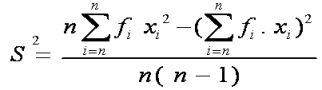



bagus
BalasHapus